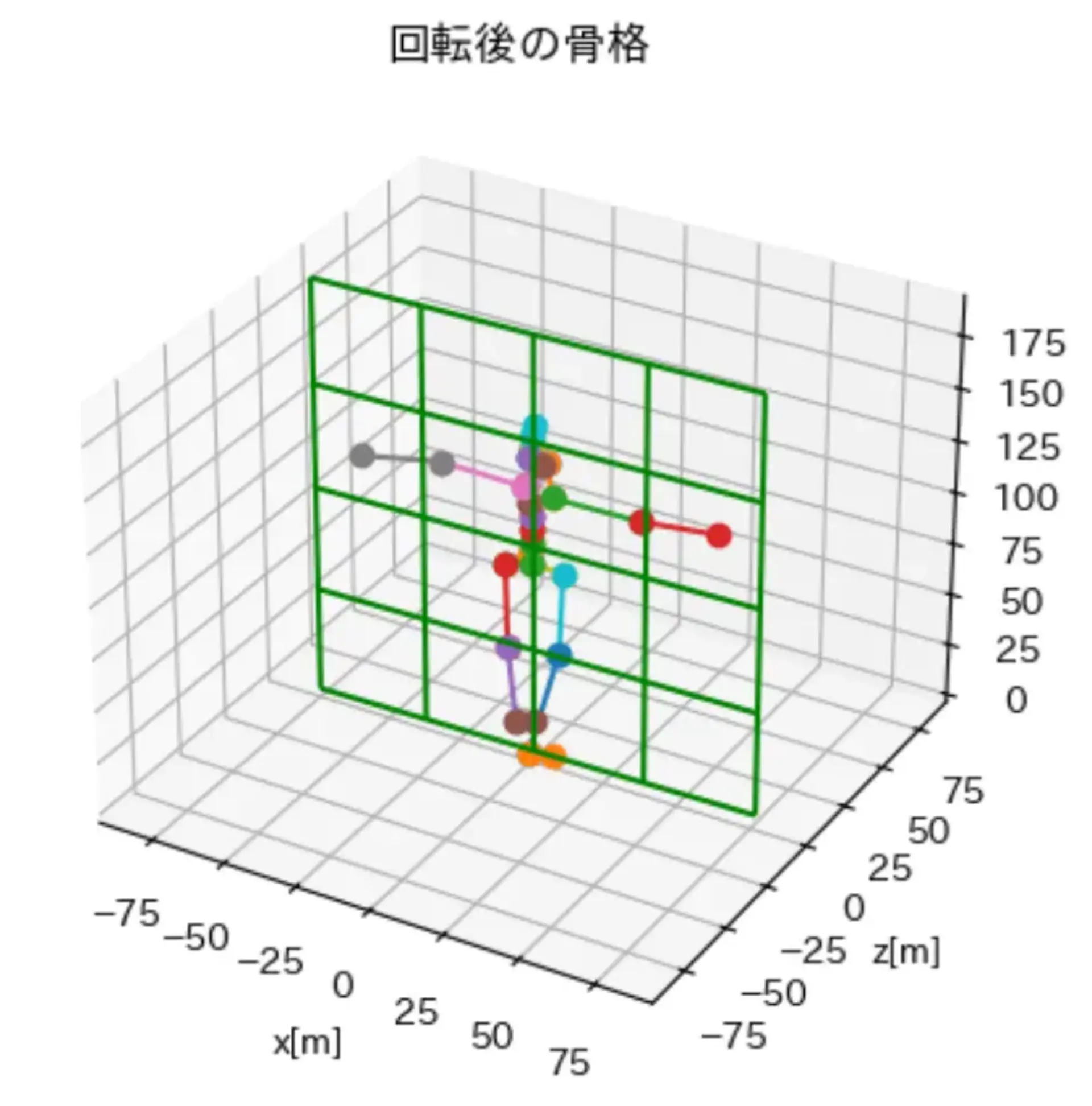
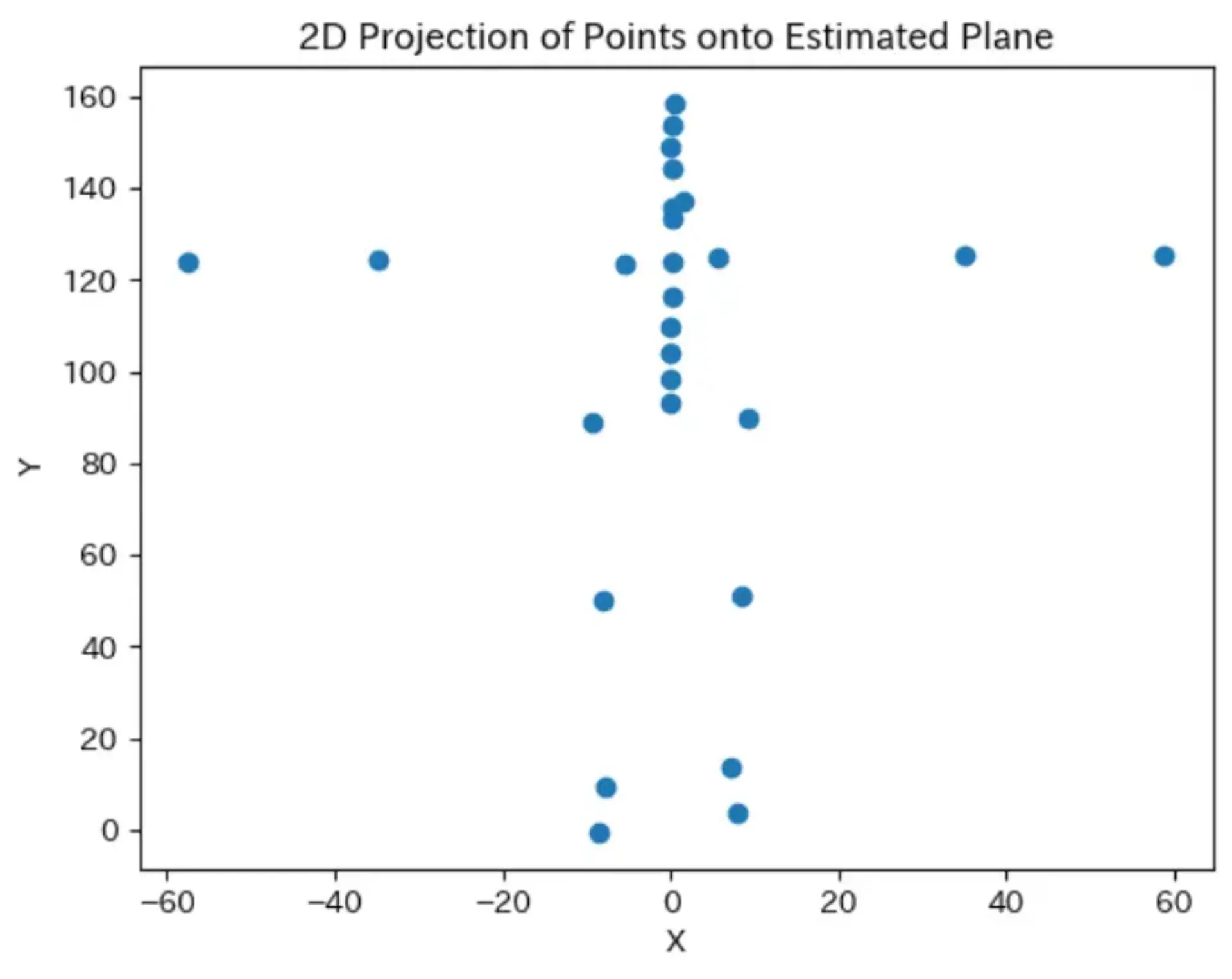
3次元空間の点を2次元平面に落とし込む
出席率
- 3年セミナー:??%
スケジュール
短期的な予定
- mocopi と お料理センシング
- シーンとランドマークを決める(~2月上旬)
- SVM で動作判別する
- 機械学習を深める
- お料理センシング
- お料理でどんな動作があるかを知る
- レシピを決める
- 関節を3次元座標に変換する
- 関節を2次元座標に変換する
- ST-GCN で動作推定
- 伊達巻きで動作推定する
- レシピ(手順書)を元に動作推定を補う
- 論文書く
- 発表
- BookWorm
- Pasori と デスクトップアプリを接続する(技術検証)
- nfc読み込み機能 & 画面を作る
- API と連携させる
- 管理者画面を作る
長期的な予定
- 6月 精度は置いておき、動作認識を完成させる
- 7月 リファクターと精度を向上させる
- 8月 仕上げ
- 9月 論文書き始め
- 10月末 論文提出
- 12月 WiNF当日
進捗報告
梶先生と話した
https://kjlb.esa.io/posts/5528
目的
料理中の動作を mocopi を使ってセンシングする。
このデータから最終的に位置推定を行う。
- 一定の区間でどの動作をしているかを当てる (クラス分類)
- 料理の手順を元にシーン検知を補正する
- 例) 焼く動作 → 卵割る動作 はおかしい
- 位置とシーンを相補的に補正する
- 例) 冷蔵庫の前で焼く動作 はおかしい
目標
12月頃の WiNF に出たい
(10月末 論文完成)
前回
平面出せた. 2次元に変換したい
2次元に落とし込むための平面を出す別の案
- y軸と並行な腰を通る直線($L_1$)を取る
- その直線から最も遠い点($P_1$)を取る
- Aから最も遠い点($P_2$)を取る
- $L_1$ と並行で $P_1$ $P_2$を結ぶ直線($L_2$) と重なる平面を使う
点を2次元平面に落とし込む
今回やりたいのは 射影変換 の中の1つぽい
- 正射影
- 投視射影
がある
https://sonson.jp/blog/2006/04/04/opengl-6/
今回は正射影
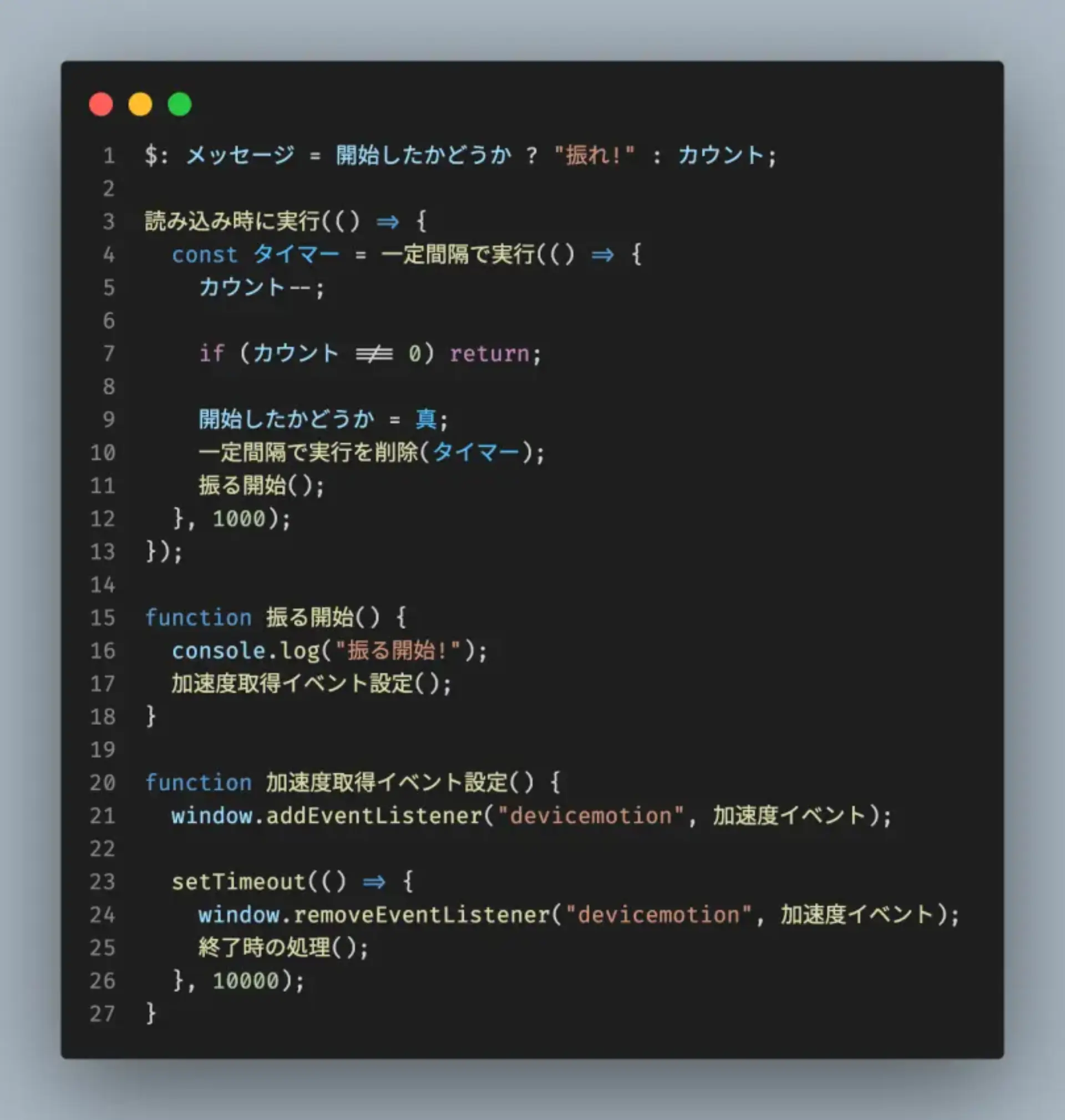
最小二乗法を使って平面に落とし込む
1# 最小二乗法による平面の推定 2Xtil = np.c_[np.ones(len(points)), points[:, 0], points[:, 1]] 3A = np.dot(Xtil.T, Xtil) 4b = np.dot(Xtil.T, points[:, 2]) 5w = linalg.solve(A, b) 6 7# 平面の方程式 8def plane_eq(x, y): 9 return w[0] + w[1] * x + w[2] * y 10 11# 平面上への点の射影 12projected_points = np.array([[point[0], point[1], plane_eq(point[0], point[1])] for point in points])
z軸を使っていないため違う. そもそも
→ 非連続的になる可能性があるためやめた
例) 腕を直角に伸ばす, 右手先が一番遠い→少しずつ縮めると左手先が一番遠くなった時平面が急激に変化する
別の案2
- 上記の図でいう xz 平面に落とし込む
- xz平面上で近似直線を引く
- y軸方向に伸ばして平面にする
二次元で考えれるためとても扱いやすい
近似直線を引く
1points = np.array([j["coord"] for j in rotated_coord.values()]) 2res = np.polyfit(points[:, 0], points[:, 2], 1) 3 4y = np.poly1d(res)(points[:, 0]) 5 6plt.scatter(points[:, 0], points[:, 2], label="元データ") 7plt.plot(points[:, 0], y, label="1次") 8plt.xlim(-60, 60) 9plt.ylim(-20, 20) 10plt.show()
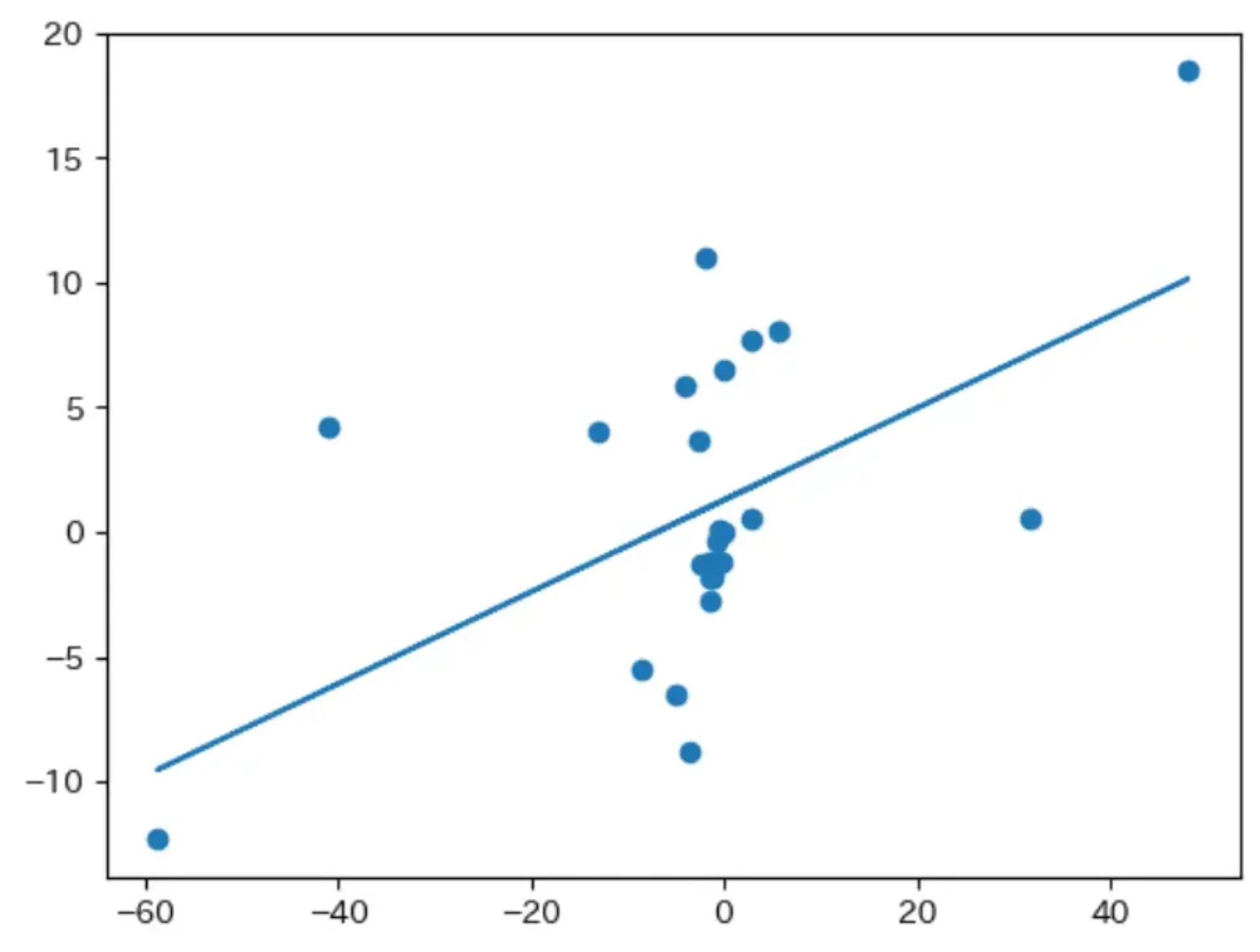
直線上に射影した
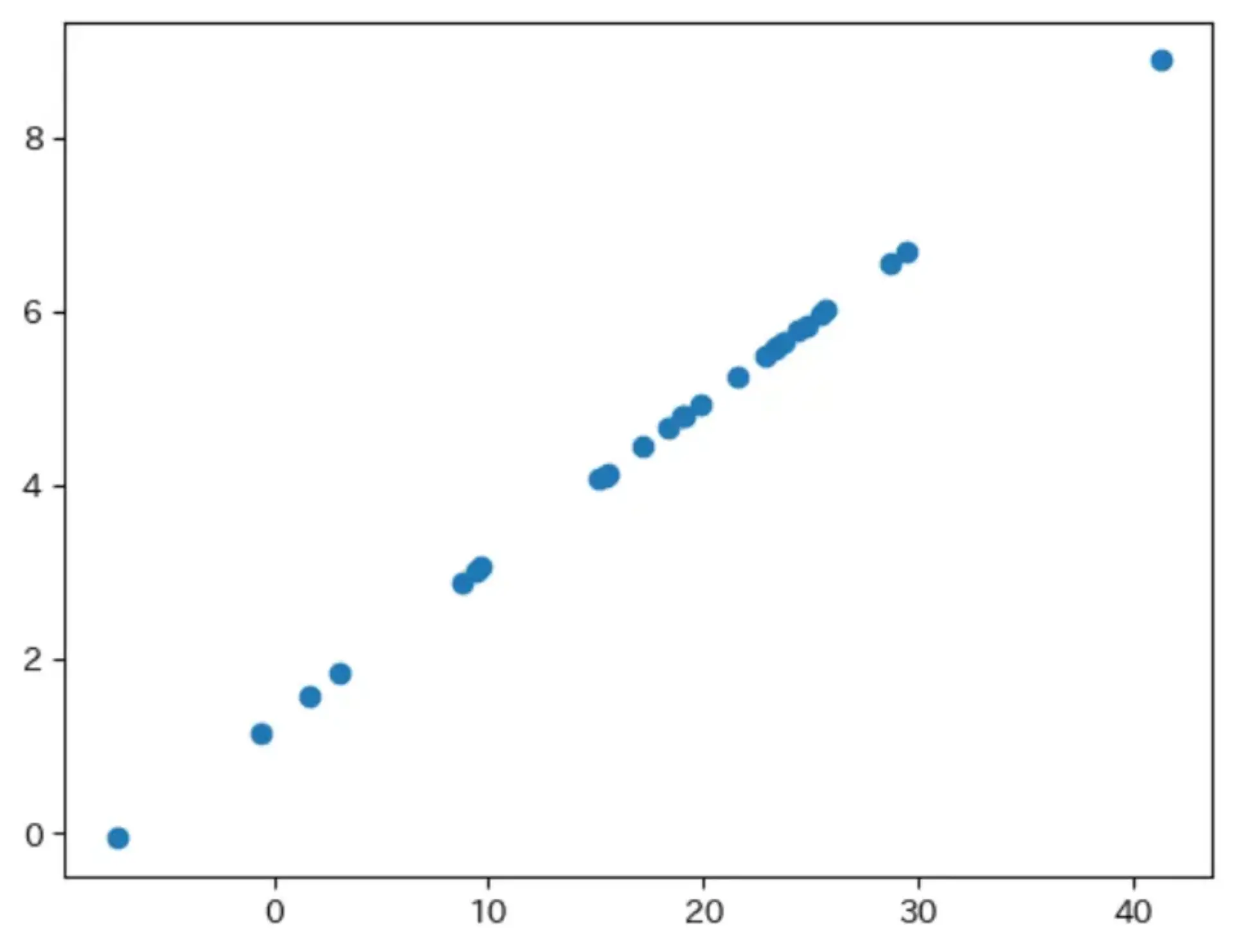
縮尺を統一
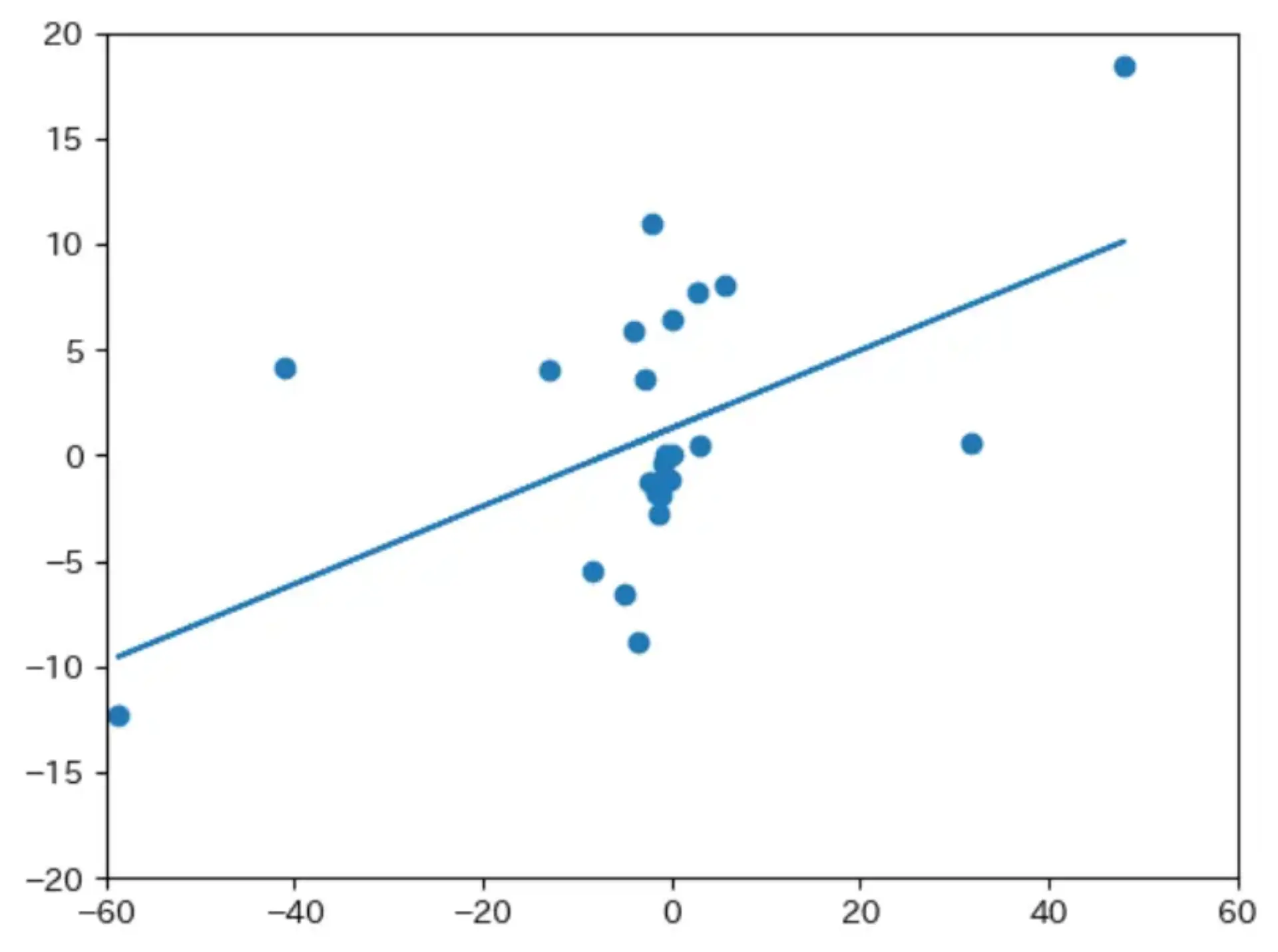
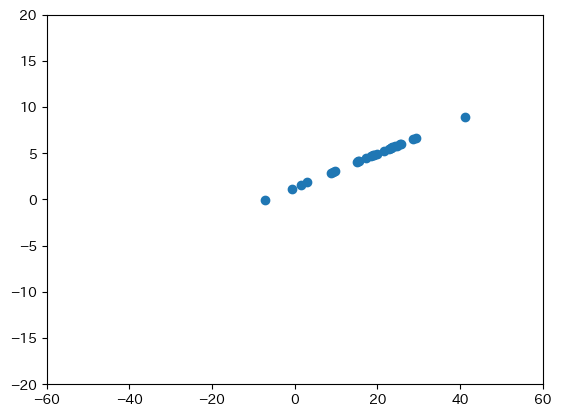
ミスってそう
自分でコードを書いてみた
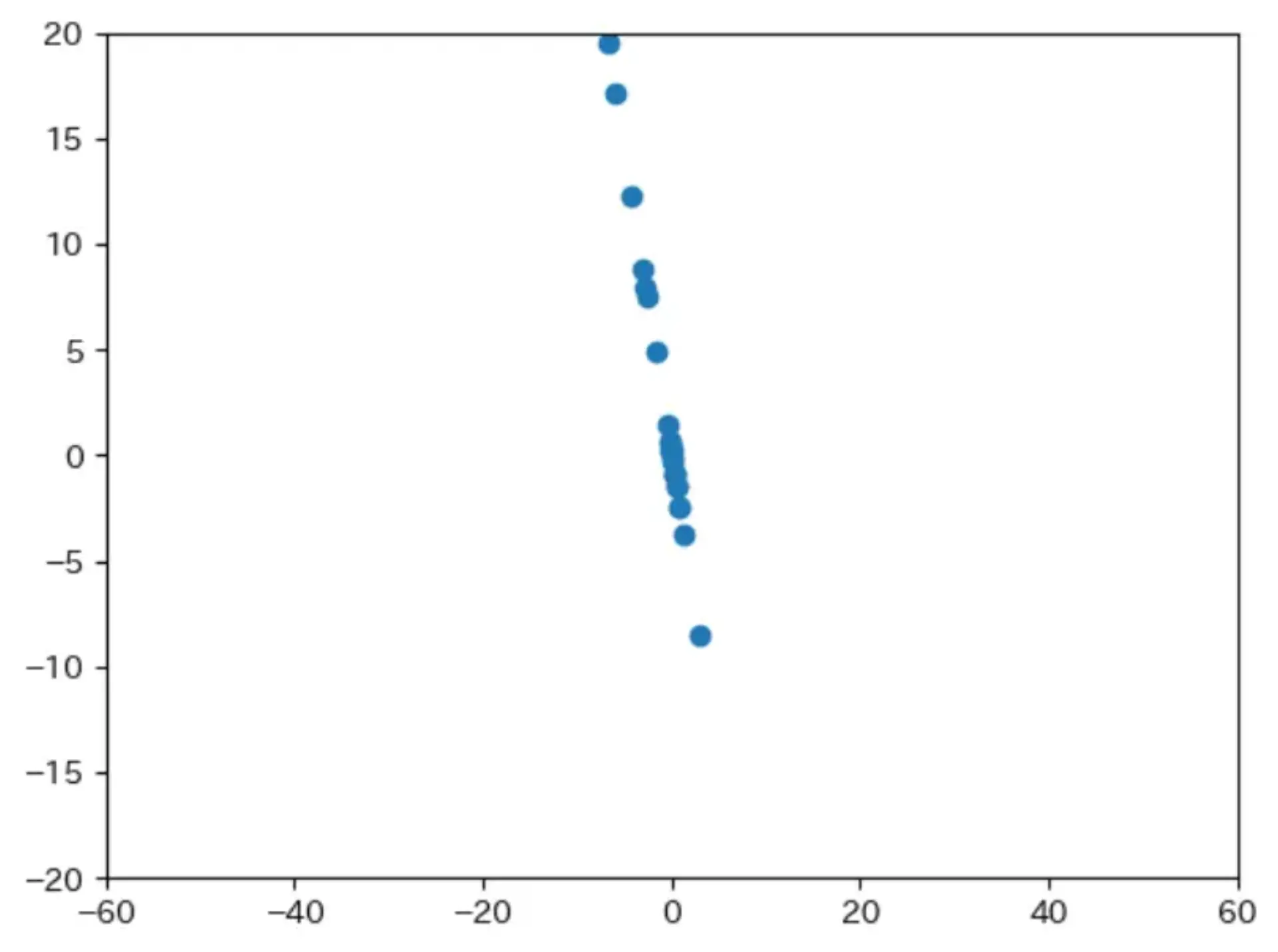
明らかに違う
中学数学を学び直した
https://www.nekonecode.com/math-lab/pages/collision2/point-and-segment-nearest/
https://www.try-it.jp/chapters-6533/sections-6534/lessons-6575/
https://manabitimes.jp/math/1137
アフィン変換すごい
数学は理解したので、Python で書いているところ
進路関係
余談
プロジェクト演習やってます